线段树浅学

doMore 34 2025-01-08

定义与概念

线段树是一种二叉树数据结构，用于高效地处理区间查询和区间修改操作。它将一个区间划分成多个子区间，每个节点都对应一个区间。
例如，对于区间 [1，10] , 线段树的根节点可能表示整个区间 [1,10] ，根节点的左子结点 可能表示 [1,5]， 右子节点表示区间 [6,10]，这种划分会持续下去，直到区间长度为 1（叶子结点）。叶子节点表示原始区间中的单个元素。

朴素思想

假设我们现在有一个数组，我们想对其一个区间查询其区间和，那么对这个数组的查询操作，及找到该区间内所有元素的和的时间复杂度为O(n)。如果我们想要更新其数组内的一个数的值，这个更新操作的时间复杂度便为O(1)，可以直接根据下标进行修改。

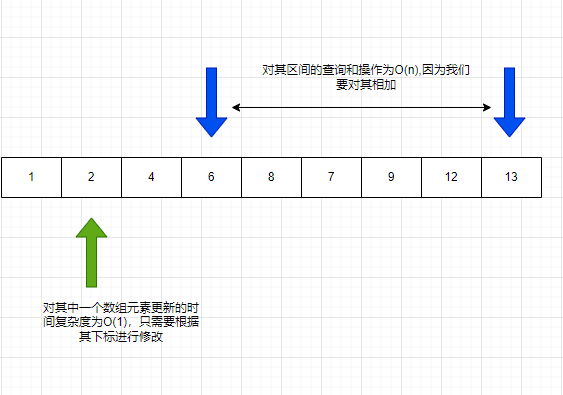
diyizhang

前缀和

提到和，尤其是对于查询区间和，我们容易想到的一个点就是使用前缀和，这样我们就可以将查询的操作提升到O(1), 但是使用前缀和会有一个问题，当我们的更新次数过多时，尤其是需要更新的元素比较靠前时，每一次更新的代价都会为O(n)，从而没有达到优化的效果。但是对于元素不变动的数组前缀和还是有很不错的优势！

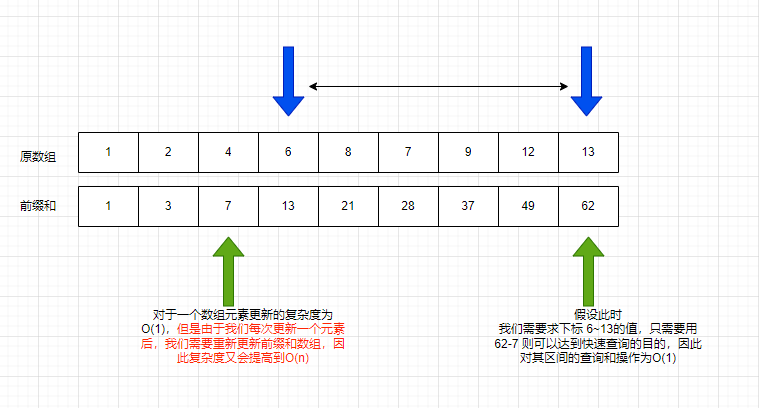
diyizhang

线段树

线段树将上述问题的查询以及更新的时间复杂度都变成了O(logn)。当进行多次查询与更新时，线段树一定比上述两种方法更具优势。
首先我们先来看一下线段树是什么结构。线段树是一棵二叉树，每个非叶子节点都有左右子节点。用数组来表示树的结构，对于根树的根节点，它会在index=1的位置上(其实此处0也行，不过大家普遍用1,区别就是计算子节点的方式不同)，然后对于其节点的左右子节点的下标分别为 2*index 与 2*index+1。

  • 每个节点除了存储表示区间的左右端点和外，还存储与区间相关的信息。
  • 例如，在求区间和的线段树中，节点存储该区间内所有元素的和。如果是求区间最大值的线段树，节点存储该区间内元素的最大值。

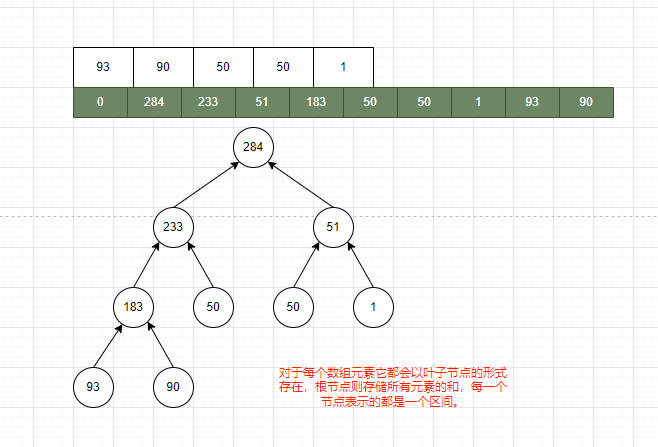
diyizhang

查询: 我们会根据区间从根节点向树的两边递归查寻。假设我们现在要查找此树的[2,4]的区间和，及[50,50,1]的和, 那么这个过程是什么样的呢？

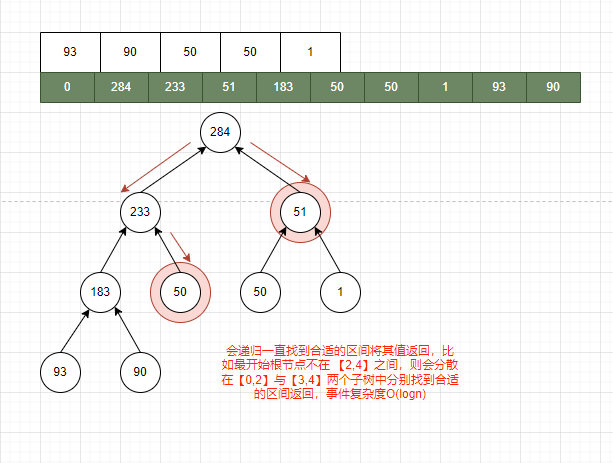
diyizhang

代码实现

建树


public static void buildTree(int[] arr, int[] tree, int start, int end, int nodeIndex) {  
// 找到叶子节点，不再递归
    if (start == end) {  
        tree[nodeIndex] = arr[start];  
    } else {  
        // 找到树的左子节点(2*nodeIndex)  
        // 找到树的右子节点(2*nodeIndex +1)  
        int leftNode = 2 * nodeIndex;  
        int rightNode = 2 * nodeIndex + 1;  
        int mid = (start + end) / 2;  
        // 将树进行分割，左右递归建树  
        buildTree(arr, tree, start, mid, leftNode);  
        buildTree(arr, tree, mid + 1, end, rightNode);  
        tree[nodeIndex] = tree[leftNode] + tree[rightNode];  
    }  
}

检索

需要分情况进行讨论：

  • 情况一
    diyizhang
  • 情况二则是当前区间被我们的检索区间包围，及蓝色区间在绿色区间里面时，因此不必继续往下递归，可以直接返回当前节点值。这里比较容易想，读者可参考之前的线段树查询。思考一下，每一个节点表示的都是一个区间内所有元素的和，那么当整个当前区间都被我们的检索区间包围了，证明我们需要所有的元素，因此不必继续往下递归查询，可以返回其节点值。
public static int query(int[] arr, int[] tree, int start, int end, int l, int r, int nodeIndex) {  
    if (l > end || r < start) {  
        return 0;  
    }  
    if (l <= start && end <= r) {  
        return tree[nodeIndex];  
    } else {  
        // 递归查询  
        int leftNode = 2 * nodeIndex;  
        int rightNode = 2 * nodeIndex + 1;  
        int mid = (start + end) / 2;  
        int leftSum = query(arr, tree, start, mid, l, r, leftNode);  
        int rightSum = query(arr, tree, mid + 1, end, l, r, rightNode);  
        return leftSum + rightSum;  
    }  
}

更新操作和建树操作很像，可以进一步思考。

应用场景

  • 区间求和问题：高效地计算给定区间内元素的和。例如，给定一个数组，频繁查询数组中某个区间内元素的和。
  • 区间最大值 / 最小值问题：快速获取给定区间内元素的最大值或最小值。比如，在一个时间序列数据中，查询某段时间内的最高温度或最低温度。
  • 动态区间更新与查询：在一些动态的数据环境中，需要同时支持区间修改（如增加一个值、修改元素）和区间查询操作，线段树能够很好地应对这种情况。
java 算法